Encontrar la matriz de una transformación lineal con respecto a la base estándar. Determinar la acción de una transformación lineal sobre un vector en \(\mathbb{R}^n\). En los ejemplos anteriores, la acción de las transformaciones lineales consistió en multiplicarse por una matriz. Resulta que este es siempre el caso de las.. 2. Matriz de una transformación lineal y cambio de base. Recordemos que si $T:\mathbb{R}^n\rightarrow\mathbb{R}^m$ es una transformación lineal existe su matriz.

TRANSFORMACIONES LINEALES ejercicios RESUELTOS paso a paso APLICACIONES LINEALES T(x,y)=(x , y

Matriz asociada a una transformación lineal en diferentes bases (V2) YouTube

Calculo de la matriz de una transformacion lineal en una base YouTube

5.3 Representacion Matricial de una Transformación Lineal

Matriz de una transformación lineal de R3 a R2 YouTube

Representación matricial de una transformación lineal r3 a r3 YouTube

MATRIZ ASOCIADA A UNA TRANSFORMACION LINEAL YouTube

Matriz de una transformación lineal a partir de sus imagenes en una base YouTube

Matriz asociada a una transformación lineal respecto de bases B1 B2 02 YouTube

Ejemplo 1 Núcleo e imagen de una Transformación lineal YouTube

2.8 Transformación Lineal 3 YouTube

Transformaciones Lineales YouTube

La Matriz de una Transformación Lineal YouTube

Representación matricial de una transformación lineal r2 a r3 YouTube
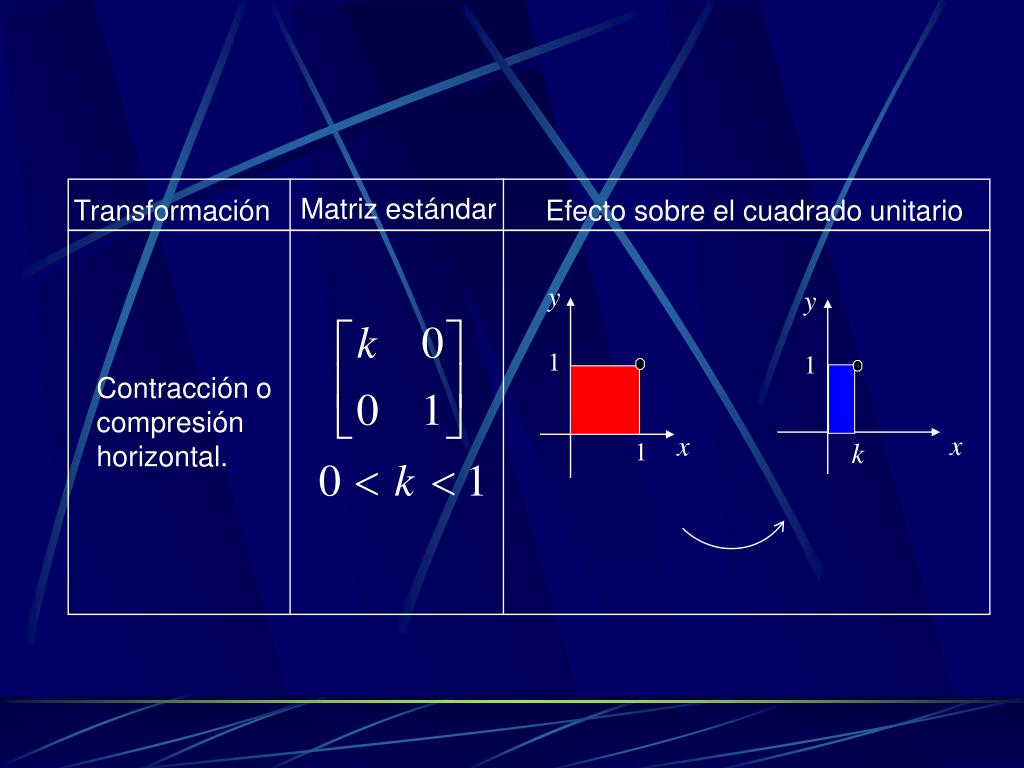
PPT Álgebra de Transformaciones Lineales PowerPoint Presentation, free download ID591839

Representación Matricial de una Transformación lineal YouTube

Transformación Lineal. Transformación Lineal Definida por una Matriz Ejercicio. YouTube
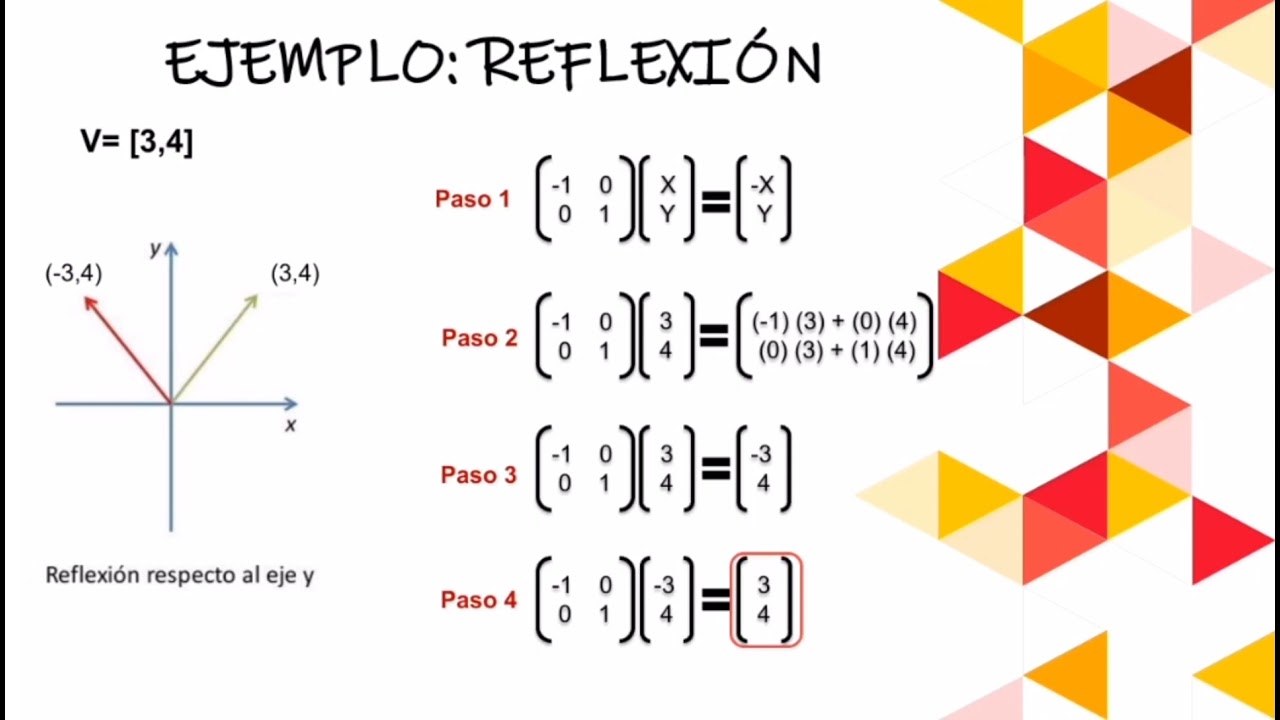
Aplicación de las Transformaciones Lineales Reflexión y Dilatación YouTube

Transformación Lineal. Imagen de una Transformación Lineal Conceptos Básicos. YouTube

Matriz asociada a una transformacion lineal
Construcción de la matriz asociada a una transformación lineal. Hemos visto ejemplos de cómo surge a partir del producto de matrices, la matriz estándar de una transformación lineal de \ ( {\mathbb {R}^n}\) a \ ( {\mathbb {R}^m}\). En lo que sigue intentaremos generalizar para cualquier espacio vectorial de dimensión finita, el concepto.. Transcripción del video. supongamos que tienes una matriz de n por n elementos que se mira algo así tienes en la primera columna el primer elemento de la primera columna es 1 y el resto de los elementos en la columna son ceros entonces tienes 10 y 000 hasta llegar al enésimo término que también es 0 ahora en la en la segunda columna tienes.