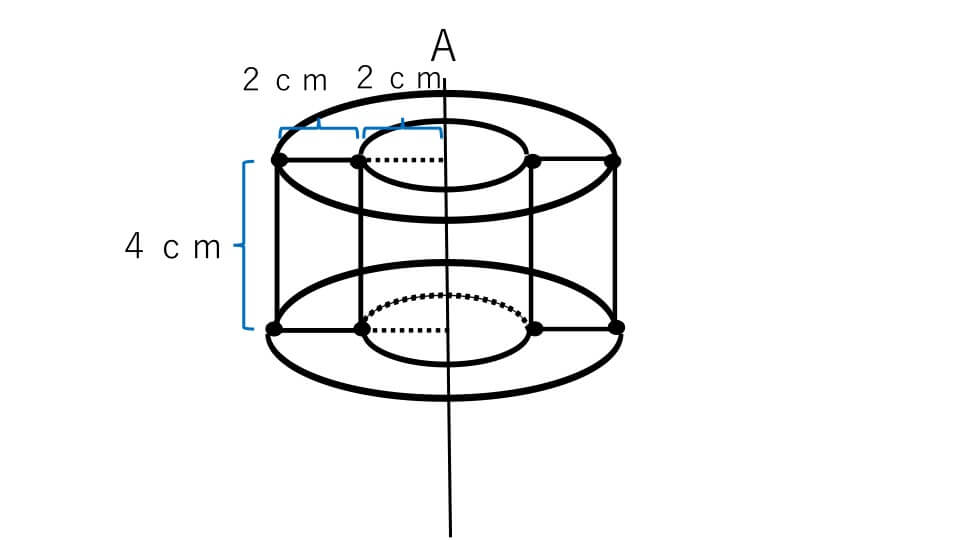
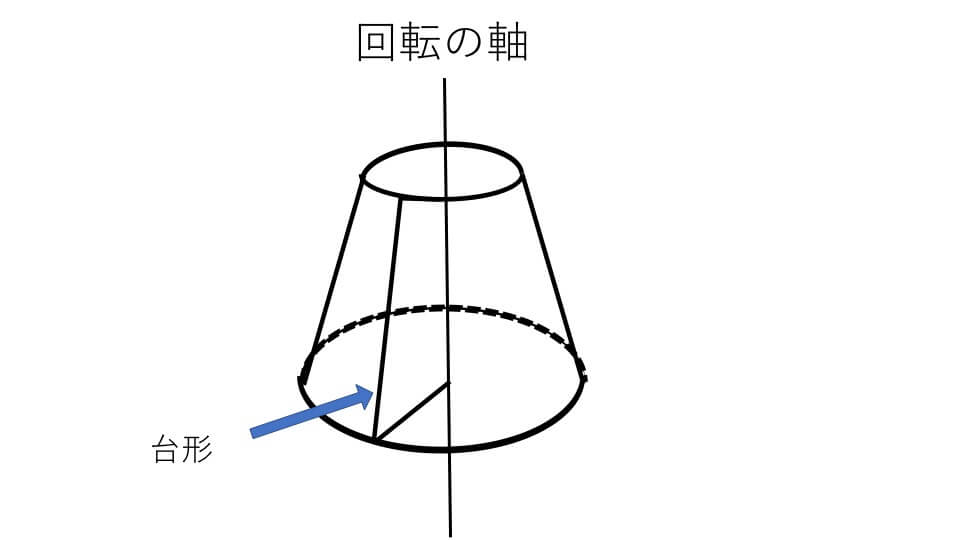
回転体の体積の求め方. 空間幾何. グラフ上の平面図形を回転させてできる立体の問題も定番なので、今のうちから慣れておきましょう。 非常に便利な定理もありますが、まずは基本をしっかり押さえておくことが肝心です。 【問題】 原点Oを通る放物線上の3点A (-1,1),B (2,4),C (1,1)。 （1） OABを直線x=0を軸として1回転させてできる立体の体積は？ （2） OABを直線ACを軸として1回転させてできる立体の体積は？ 3点は、別に放物線上の点でなくてもいいのですが、放物線上の点として出題されることが多いです。 （傾きやy切片を簡単に求められるからですね。 (答え; 82 π/ 27,9 π/ 2) 【解答（1）】 まず、 直線ABとy軸との交点をD、. 回転体の体積を求める① ～体積比のすすめ～ みなさん、こんにちは。 受験Dr.算数・理科科の川上と申します。 今回は回転体について触れていきます。 下の図のような三角形をℓを軸に回転すると円すいに. 長方形を回転させると円柱になります。 見たことのある人も多いのではないでしょうか。 慶應中等部のように出題頻度の高い学校もいくつかあり、押さえておきたいテーマの一つです。 （慶應中等部の回転体は表面積を求めるケースがほとんどですが） 今回は体積を求めるために、体積比を活用する考え方を紹介します。 （問題①） 下の台形を、ℓを軸に1回転したときにできる立体の体積を求めなさい。 慣れないうちは見取り図を描きましょう。 以下のような円すい台になります。

中1数学 空間図形 回転体(体積) YouTube

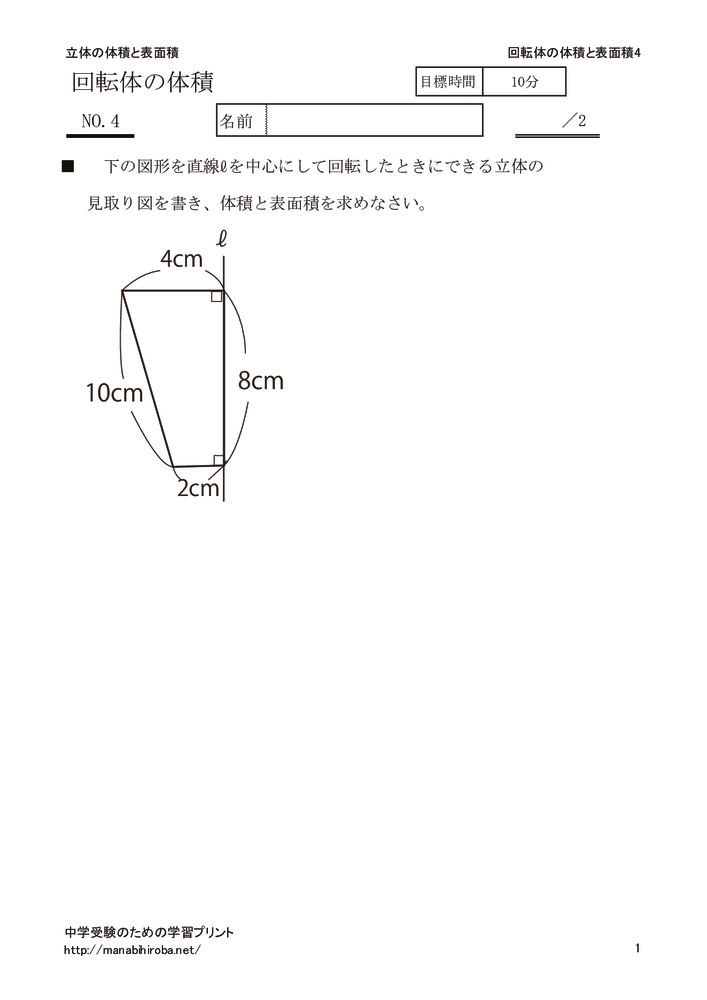
回転体 中学受験準備のための学習ドリル

積分計算による体積の求め方！断面積の積分や回転体の体積 受験辞典

【中学受験算数】まいにち算数056 回転体の体積(2001年灘中) YouTube

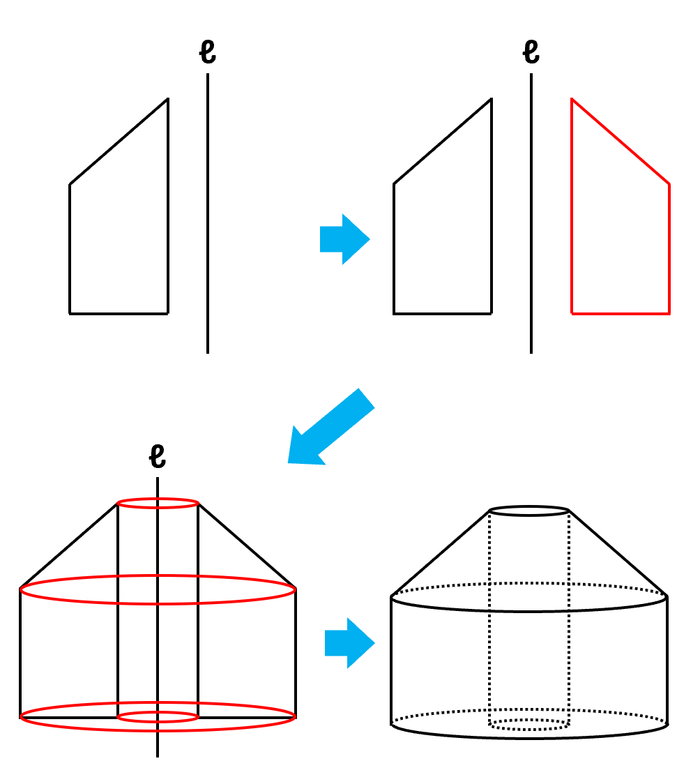
回転体の体積をどうやって求める？ 複雑な立体も工夫して計算すれば難しくない 中学受験ナビ

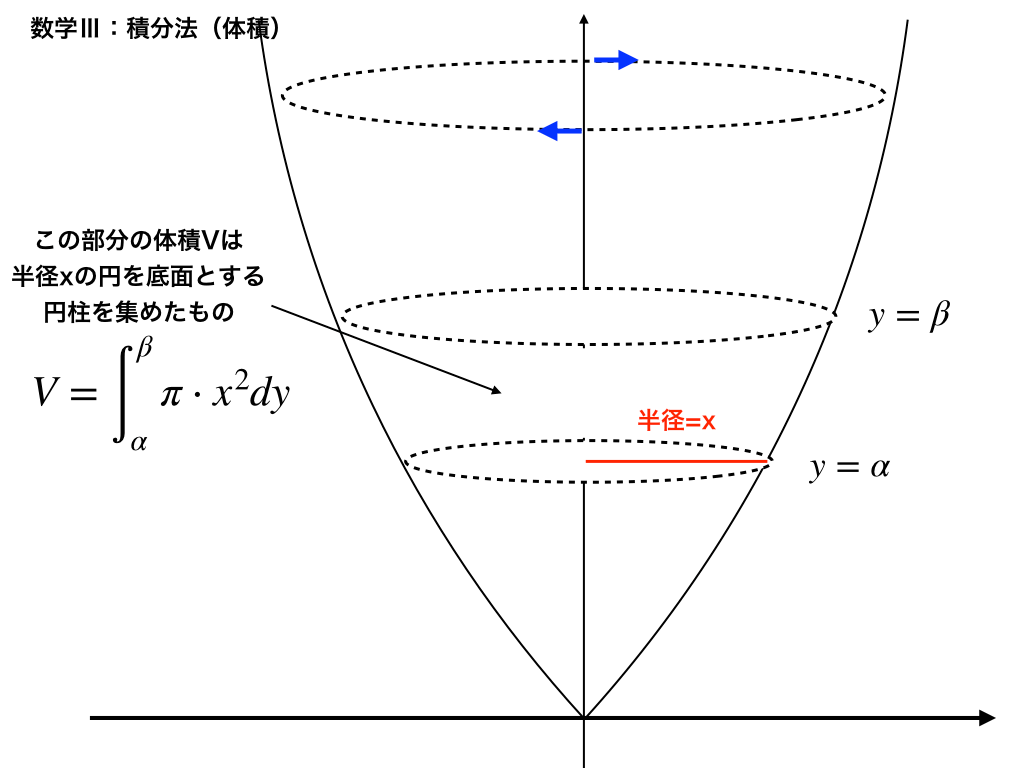
x軸についての回転体の体積の求め方とコツを分かりやすく解説!

【中学受験算数】立体図形 回転体の体積 2015年 洛星中【最難関クラス/偏差値up】 YouTube

【高校数学Ⅲ】「y軸の周りの回転体の体積」 映像授業のTry IT (トライイット)

【中学数学】回転体の見取り図の書き方がわかる4ステップ Qikeru：学びを楽しくわかりやすく

回転体～円錐の体積と表面積の求め方 現役塾講師のわかりやすい中学数学の解き方

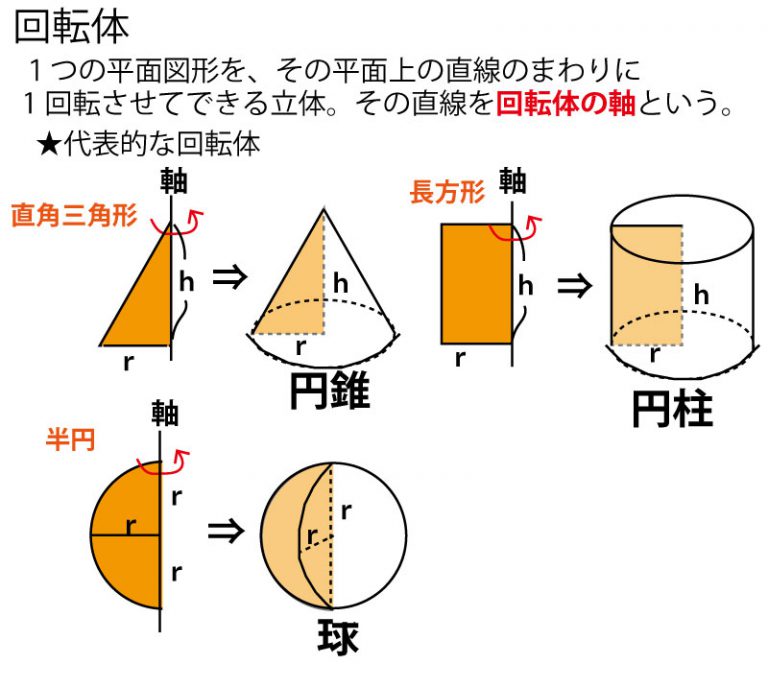
2015年前期、千葉県公立高校入試「数学」第2問（3）（回転体の体積）解答・解説 船橋市議会議員 朝倉幹晴公式サイト

中学受験 算数 回転体 〜3ステップの書き方を覚えて攻略〜

立方体を対角線を軸として回転させた回転体の体積 YouTube

國學院大學久我山中学校－2019年度算数大問2(7)回転体の体積－過去問解説 中学受験ナビ

【高校数学Ⅲ】「x軸の周りの回転体の体積」(問題編1) 映像授業のTry IT (トライイット)

[裏ワザ] パップスギュルダンの定理・回転体の体積 YouTube

回転体の体積の求め方 数学カフェjr.

中学受験 算数 回転体 〜3ステップの書き方を覚えて攻略〜 中学受験アンサー

回転体の体積 御三家中学受験・桜蔭・開成・東大サピックス家庭教師・ファインウェブ 楽天ブログ

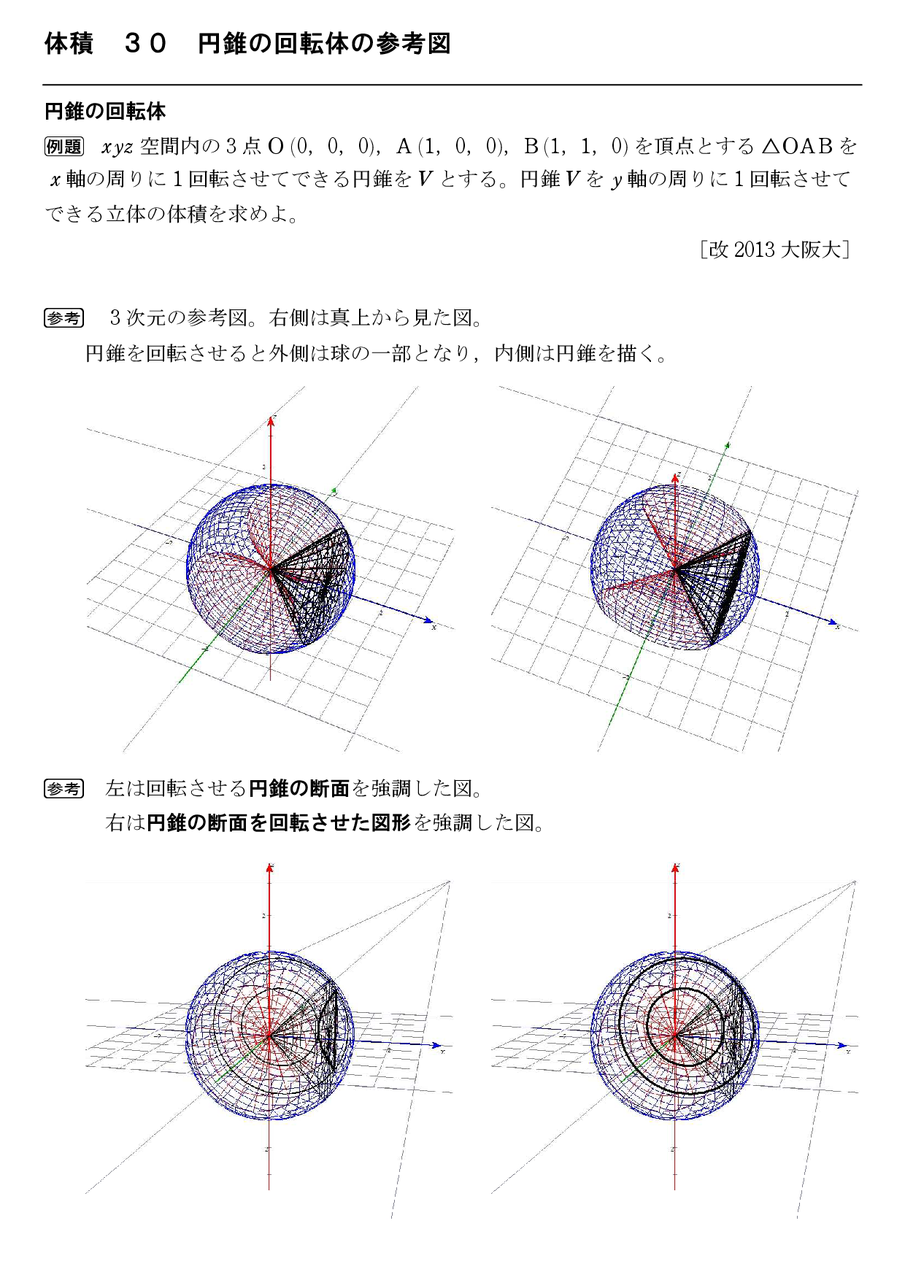
体積 30 円錐の回転体の参考図 怜悧玲瓏 ～高校数学を天空から俯瞰する～

x x 軸の周りの回転体の体積. y = f (x) y = f ( x) と x x 軸，および2直線 x = a x = a と x = b x = b で囲まれた部分を， x x 軸の周りに1回転してできる立体の体積 V V は. V = ∫ b a {f (x)}2πdx V = ∫ a b { f ( x) } 2 π d x. 断面は半径が |f (x)| | f ( x) | の円になるので， 定積分で求める体積 によると上の公式になるのは明らかです．. 断面が円というよりドーナツ状になる応用問題もあるので，上の公式丸暗記というより断面積を積分する考え方が重要です．. 例題と練習問題. 次で囲まれた部分を x x 軸の周りに1回転してできる立体の体積 V V を求めよ．.. 【体積】 全体の円柱から、空洞部分の円錐を引けばよいので $$(円柱)=(5\times 5\times \pi)\times 9=225\pi(cm^3)$$ $$(円錐)=(5\times 5\times \pi)\times 9\times \frac{1}{3}=75\pi(cm^3)$$ 以上より全体の体積は $$225\pi-75\pi=\color